
1. 베이즈 확률
베이즈 확률은 확률을 주장에 대한 신뢰도로 해석하는 확률론입니다. 예를 들어 동전의 앞면이 나올 확률이 50%라고 한다면 빈도주의적 확률론 관점에서는 "동전을 10번을 던졌을 때 5번 앞면이 나온다"라고 해석하는 반면, 베이즈 확률론 관점에서는 "동전의 앞면이 나올 가능성이 50%이다"라고 해석합니다.로지스틱 회귀에서 설명한 최대우도추정법도 확률에 대한 가능성인 우도(likelihood)의 최대값을 통해 확률을 추정했습니다. 즉, 우도는 베이즈 확률이라 볼 수 있습니다.
베이즈 확률을 사용하여 두 조건부 확률 사이의 관계를 정의한 것을 베이즈 정리라고 합니다. 베이즈 정리의 공식은 다음과 같습니다.
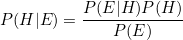
P(H)와 P(E)는 사전확률이며, 관측자가 이미 알고 있는 사건으로부터 나온 확률입니다.
P(E|H)는 이미 알고있는 사건(H)이 발생했다는 조건하에 다른 사건(E)이 발생할 확률 입니다. 우도(likelihood)와 동일합니다.
P(H|E)는 사후확률이며, 사전확률과 우도를 통해 알게되는 조건부 확률입니다.
베이즈 정리는 다음과 같이 다이어그램으로부터 유도됩니다.
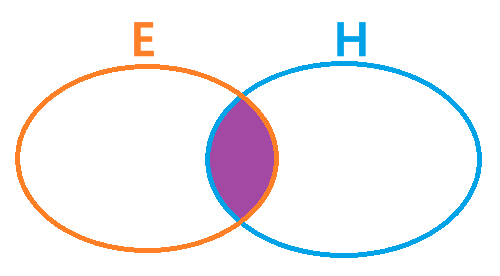
다이어그램은 다음과 같은 식으로 나타낼 수 있습니다.
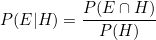
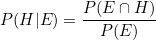
두 연립방정식을 합치면 베이즈 정리의 공식과 같습니다.
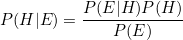
다음은 영화 21에 나온 몬티홀 문제입니다.

빈도주의적 확률에서는 둘 중 하나에 자동차가 있으므로 선택을 바꾸던 바꾸지 않던 자동차를 가질 확률은 50%가 됩니다. 그러므로 대다수 사람들은 심리적인 이유로 문을 바꾸지 않게 됩니다.
그러나 베이즈 확률은 다릅니다. H = "자동차를 선택", E = "사회자가 문을 엶" 이라고 한다면 선택을 바꿨을때와 바꾸지 않았을 때의 P(H|E)를 각각 구할 수 있습니다. 사회자는 염소가 있는 문을 열게 되므로 P(E) = 1/2, 자동차는 3개 중 1개의 문에 존재하므로 P(H) = 1/3로 고정됩니다. 각각 사전확률에 해당합니다. 이제 각각의 우도 P(E|H)를 구하면 사후확률 P(H|E)를 구할 수 있습니다.
먼저 선택을 바꾸지 않은 경우에는 사회자는 염소가 있는 나머지 두 개의 문 중 하나의 문을 열게 되어 P(E|H) = 1/2 이므로 P(H|E) = (1/2) * (1/3) / (1/2) = 1/3 이 됩니다.
선택을 바꿨을 경우 사회자는 정해진 하나의 문밖에 열지 못하므로 P(E|H) = 1 이므로 P(H|E) = 1 * (1/3) / (1/2) = 2/3 가 됩니다.
그러므로 선택을 바꾸어 자동차가 선택될 확률(66.6%)이 선택을 바꾸지 않고 자동차가 선택될 확률(33.3%)보다 크므로 선택을 바꾸는 것이 유리하게 됩니다.
2. 나이브 베이즈
베이즈 확률을 기반으로 하는 분류를 나이브 베이즈 분류(Naive Bayes Classification) 라고 합니다. 예제를 통해 동작방식을 알아보겠습니다.
우선 아래와 같이 데이터셋을 만듭니다. 해당 데이터셋은 날씨에 대한 축구 경기 여부를 나타냅니다. 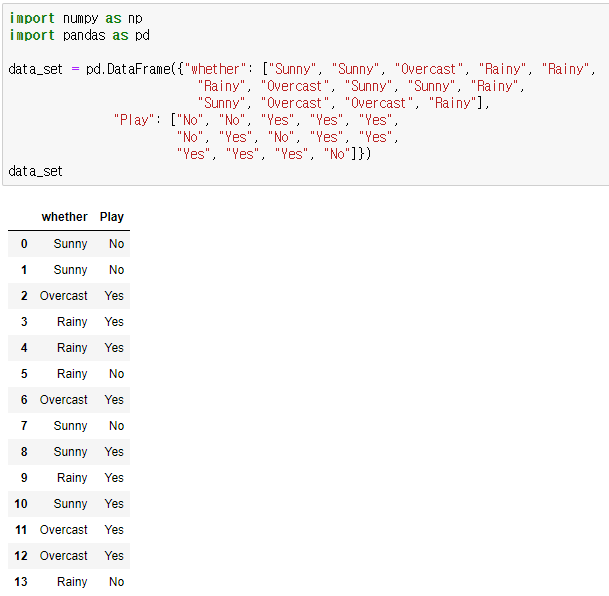
해당 데이터를 빈도를 기준으로 하여 그룹을 형성합니다. 
해당 테이블을 통해 사전확률과 우도를 각각 구할 수 있습니다.
P(Overcast) = 4/14 P(Rainy) = 5/14 P(Sunny) = 5/14 P(No) = 5/14 P(Yes) = 9/14
P(Overcast | Yes) = 4/9 P(Overcast | No) = 0/5 P(Rainy | Yes) = 3/9 P(Rainy | No) = 2/5 P(Sunny| Yes) = 2/9 P(Sunny| No) = 3/5
사전확률과 우도를 통해 사후확률을 구할 수 있습니다.
P(Yes | Overcast) = (4/9) * (9/14) / (4/14) = 0.98
P(No | Overcast) = (0/5) * (5/14) / (4/14) = 0
날씨가 Overcast인 경우 경기를 할 확률이 더 높으므로 "Yes"로 분류됩니다. 나머지도 동일한 형식으로 분류가 됩니다.
3. 파이썬 연습
Enron 이메일 데이터셋을 통해 스팸분류를 해보겠습니다.
다음 경로를 통해 다운로드 가능합니다. http://www.aueb.gr/users/ion/data/enron-spam/preprocessed/enron1.tar.gz
압축을 풀면 하위폴더에 'spam'과 'ham'이 있습니다. spam 하위경로에는 스팸 데이터가, ham 하위경로에는 정상 데이터가 txt 파일로 기록되어 있습니다. 각각의 데이터를 변수 emails에 저장하고 스팸인경우 1, 정상인경우 0이라는 라벨을 변수 labels에 저장합니다. 
자연어 처리를 위한 nltk 모듈을 사용하겠습니다. nltk 모듈을 통해 이름과 워드넷 데이터를 다운로드하고 변수 all_names에 이름을 저장합니다. 그 후 WordNetLemmatizer 함수를 통해 어간추출기를 생성하여 불용어 처리를 합니다. 전처리된 데이터는 변수 cleaned_emails 에 저장합니다. 
사이킷런 모듈의 train_test_split 함수를 통해 이메일 데이터를 훈련 데이터와 테스트 데이터로 나누고 CountVectorizer 함수를 통해 이메일 데이터의 단어를 희소행렬로 나타냅니다.
훈련 데이터는 fit_transform 메소드를 통해 훈련후 변환하고, 테스트 데이터는 transform 메소드를 통해 바로 변환합니다. 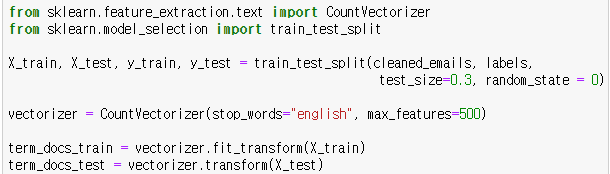
빈도기반 나이브 베이즈 분류모델은 사이킷런 모듈의 MultinomialNB 함수를 통해 생성할 수 있습니다. 하이퍼 파라미터 alpha는 초기 빈도수를 나타냅니다. 초기 빈도수가 0이면 우도가 0이 되어 분류가 안될 수 있으므로 초기 빈도값을 1로 설정하여 복잡도를 감소시킬 수 있는데 이것을 라플라스 스무딩(Laplace smoothing) 이라고 합니다. 하이퍼 파라미터 fit_prior은 사전확률을 훈련모델에 적용할지를 설정합니다. 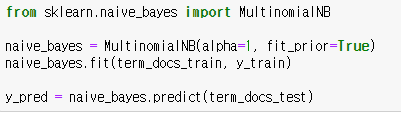
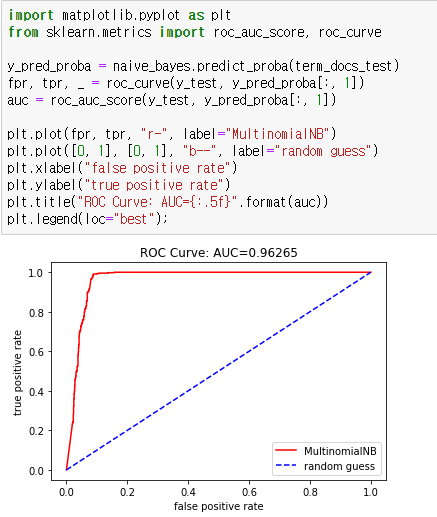
확률기반 모델이므로 AUC 곡선을 통해 성능을 평가할 수 있습니다.
|  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟