
경사하강법(Gradient Descent)은 기본적인 함수 최적화(optimization) 방법 중 하나입니다. Steepest Descent 방법이라고도 불립니다. 여기서 최적화란 함수의 최대값 또는 최소값을 찾는것을 말합니다.
앞서 모델을 평가하는 방법으로 손실함수(loss function)를 통해 평가하는 방법이 있다고 했습니다. 예를 들어 선형회귀모델에서는 MSE를 통해 모델을 평가하는데 MSE의 최소값이 최적의 모델이 됩니다. 이때 MSE의 최소값은 MSE를 미분하여 그라디언트가 영벡터가 되는 지점을 찾았습니다.
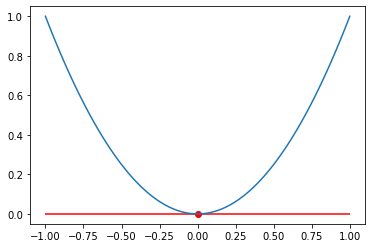
이 경우 비용함수가 이차함수로 비교적 단순하여 미분값이 0인 지점을 기준으로 최소값을 찾을 수 있었지만 다음과 같은 함수가 있을 수 있습니다.
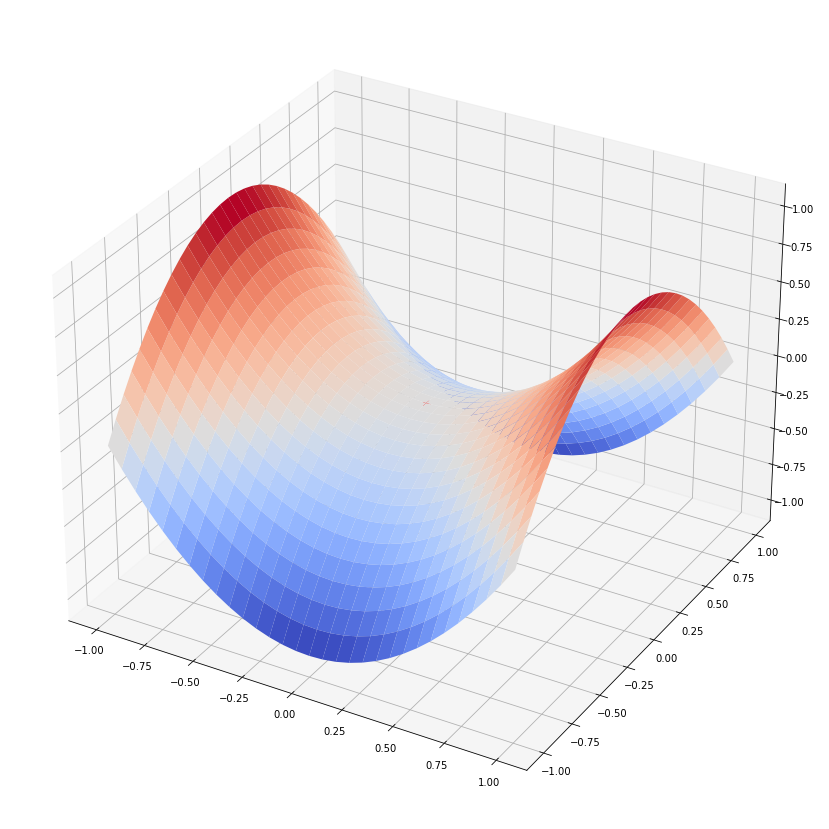
x축과 z축은 z=x2 의 관계에 있고 y축과 z축은 z=-y2 의 관계에 있을때 (0,0,0)에서 그라디언트는 영벡터가 됩니다. 그러나 x와 z의 관계에서는 최소값이지만 y와 z의 관계에서는 최대값이 됩니다. 이런 지점을 안장점(saddle point)라고 하는데 안장점이 최적화된 지점이라고 볼 수 없습니다.
로지스틱 회귀 모델 역시 그라디언트 벡터에 대한 수식이 파라미터에 대하여 비선형 관계에 있어서 파라미터를 쉽게 구할 수 없습니다.
이 경우 수치적 최적화 방법을 통해 반복적으로 파라미터를 구함으로써 최적의 파라미터를 찾을 수 있는데 대표적인 방법으로 경사하강법이 있습니다.
1) 경사하강법의 유도
등산의 경우 산 꼭대기에서 최저점으로 하산하려면 비탈길을 타고 계속 내려오면 됩니다. 이와 마찬가지로 비용함수도 경사(기울기)가 아래로 향하는 방향으로 계속 이동하다보면 비용함수의 최저점에 도달하게 됩니다.
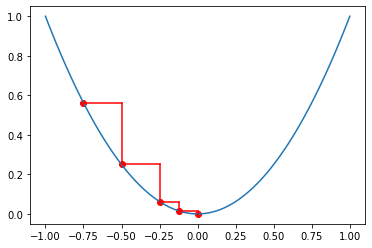
초평면에 대한 기울기는 그라디언트(gradient, ∇)라고 합니다. 비용함수의 독립변수 xi 가 그라디언트에 비례하는 값만큼 이동한 경우 그라디언트 방향과 x의 이동방향은 기호가 반대입니다. 위에 그래프를 보면 x가 음수인 경우에는 그라디언트가 (-) 방향이며, x는 (+) 방향으로 이동하게 됩니다. 반대로 x가 양수라면 그라디언트의 방향은 (+) 이며, x는 (-) 방향으로 이동하게 됩니다. 식으로 표현하면 다음과 같습니다.
xi +1 = xi - 그라디언트 방향 * 이동거리
이동거리는 그라디언트에 비례하므로 그라디언트가 크면 x는 크게 증가하고 그라디언트가 작으면 x는 작게 증가합니다. 또한 학습률(learn rate)라고 불리는 그라디언트에 비례하는 값 α 에 의해 이동거리를 조절할 수 있으므로 다음과 같은 식으로 표현됩니다.
xi +1 = xi - α∇f(xi)
그라디언트는 미분값이므로 다음과 같이 표현할 수도 있습니다.
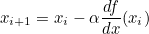
2) 하이퍼 파라미터의 설정
경사하강법에 있어서 학습률을 조절하여 학습 속도를 증가시킬 수 있습니다. 그러나 step size가 너무 커버리면 함수값이 커지는 방향으로 최적화가 됩니다.
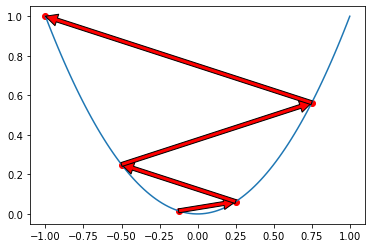
반대로 step size가 너무 작으면 학습시간이 오래 걸리고 최적의 x에 수렴하지 못할 수도 있으므로 적절한 step size를 설정해주어야 합니다.
3) 문제점
경사하강법의 경우 다음 그래프와 같이 local minima에 빠지는 경우가 생길 수도 있습니다.
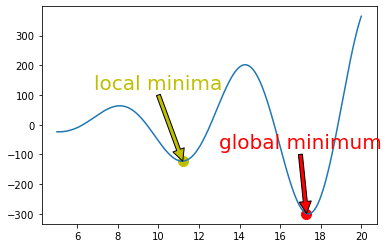
위 그래프를 보면 최소값은 global minimum 이지만 x의 시작점이 10이라면 local minima에 빠져 모델 성능이 나빠질 수 있습니다.
그러나 MSE의 경우 볼록 함수(convex function)로 local minima에 빠질 가능성이 없으며, 고차원의 공간에서는 local minima에 빠질 가능성이 현저히 낮으므로 큰 문제가 되지 않습니다.
4) 파이썬 연습
비용함수가 f(x) = 3x2 인 경우 경사하강법을 통해 최소점을 찾는 과정을 보겠습니다. 
FuncAnimation 함수는 gif 파일을 생성하기 위해 사용했습니다. 중요한 부분은 for문 입니다. 3x2 의 그라디언트는 6x 이므로 학습률(lr)이 0.001이라면 x를 x - 0.001 * 6x 씩 업데이트 합니다. 업데이트 과정을 10000번 반복하면 f(x)는 최소점 0에 가까워집니다. 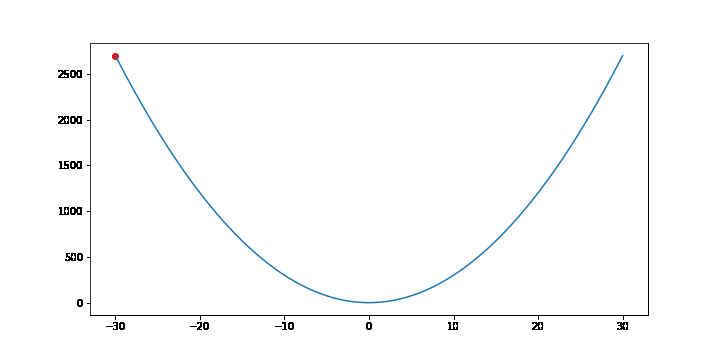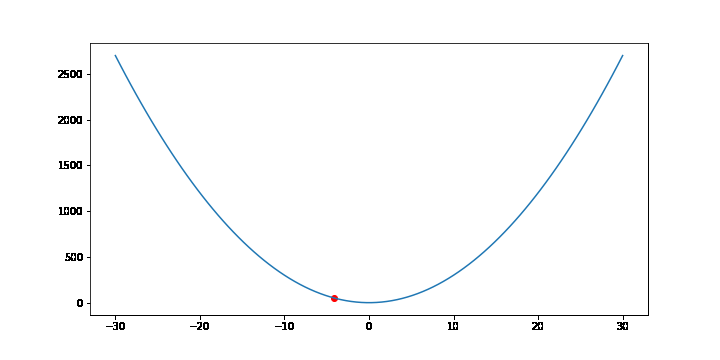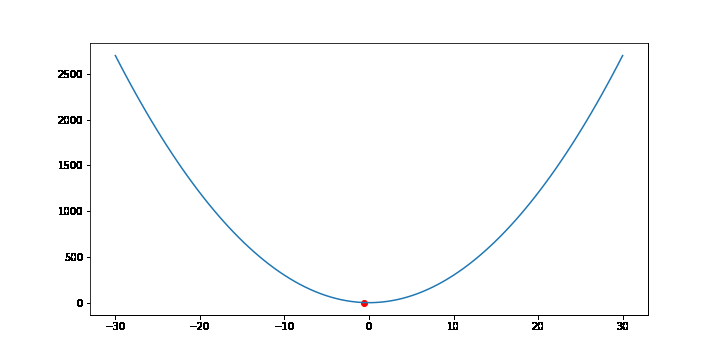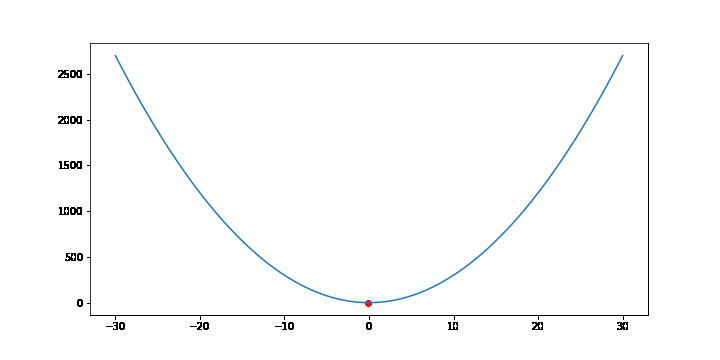
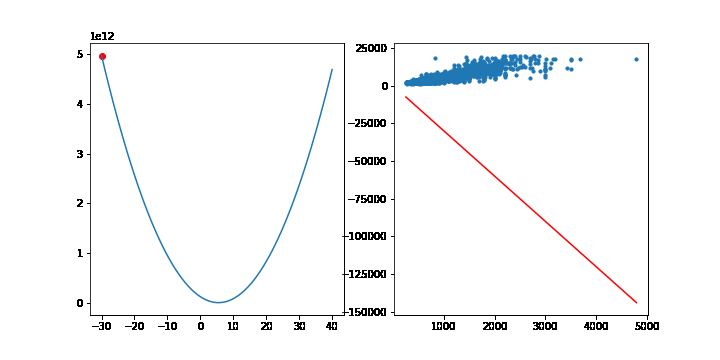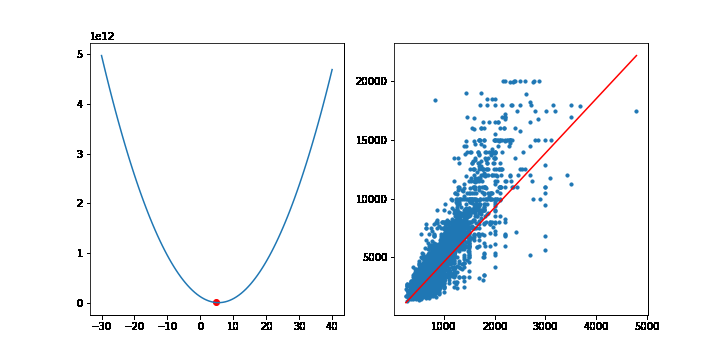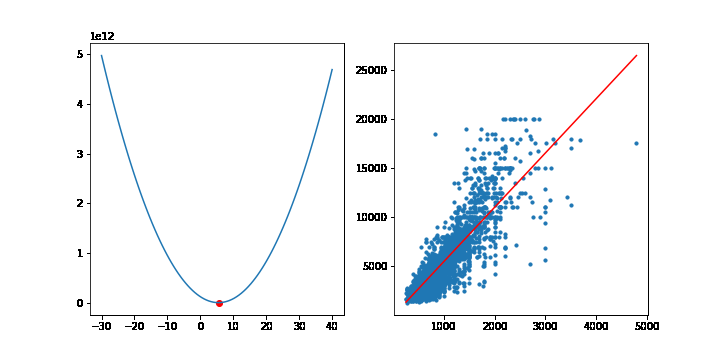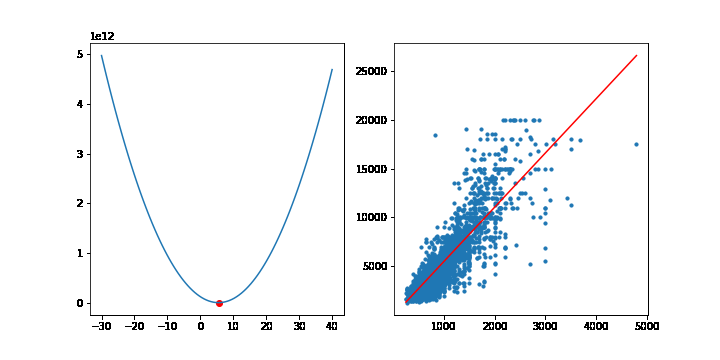
이번에는 선형모델에서 MSE의 최소점을 경사하강법을 통해 찾아보겠습니다. 이전에 선형회귀모형에서 사용한 맨허튼 집값 데이터를 사용하겠습니다.
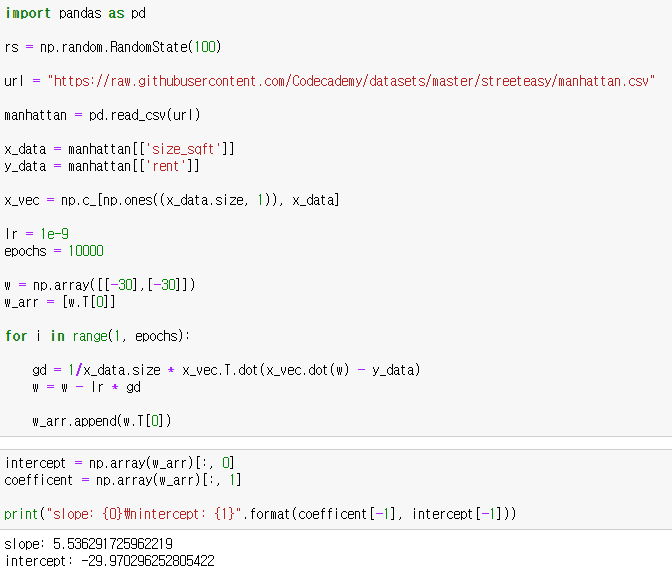
학습률은 10-9 으로 설정하고, 10,000번 반복하겠습니다. 그라디언트의 계산은 행렬을 사용하겠습니다. 이전에 설명했듯이 그라디언트는 다음 공식을 통해 계산됩니다.
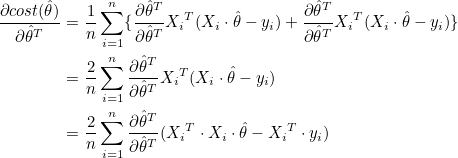
그라디언트의 상수 2는 학습률에 포함될 수 있으므로 2대신 1을 적어줍니다. 학습이 반복될때마다 가중치 w는 갱신됩니다. 그래프를 그리기위해 가중치 w를 list로 따로 모아둡시다.
아래 코드는 gif로 변환하는 코드입니다. 
이번에는 로지스틱 회귀 모델에서 경사하강법을 통해 파라미터를 찾아보겠습니다. 로지스틱 회귀에서는 MLE의 최대값에서 최적화 모델이 되므로 MLE의 음수값에서 최소값이 되는 모델을 찾으면 됩니다.
그라디언트는 다음과 같습니다. 그라디언트에 음수(-)를 붙여주면 됩니다.
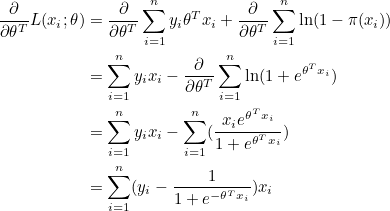
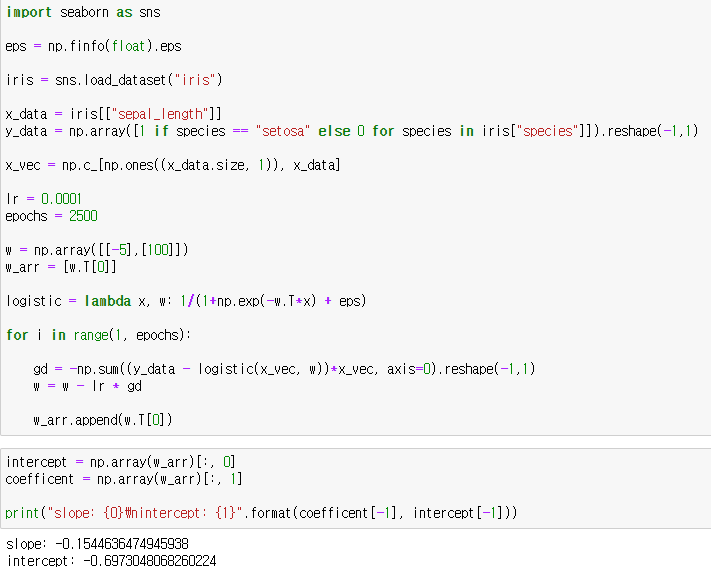

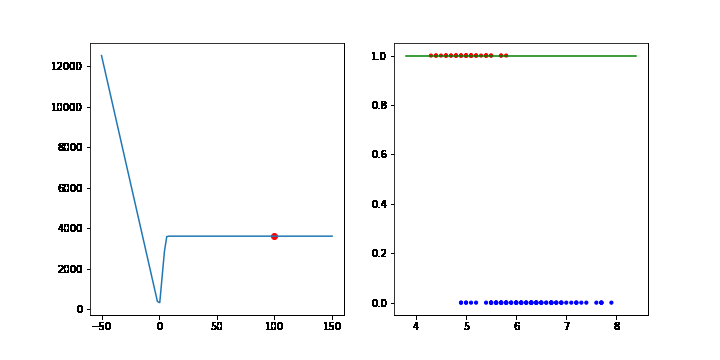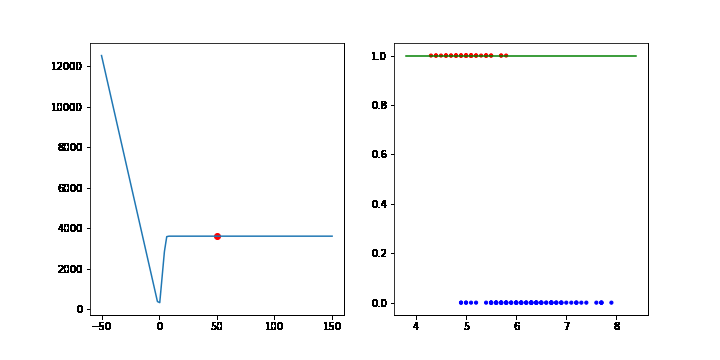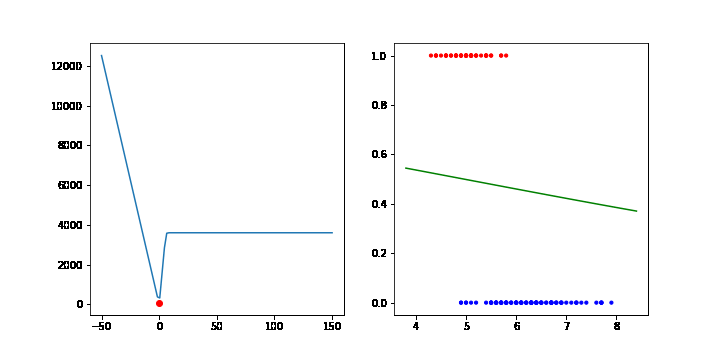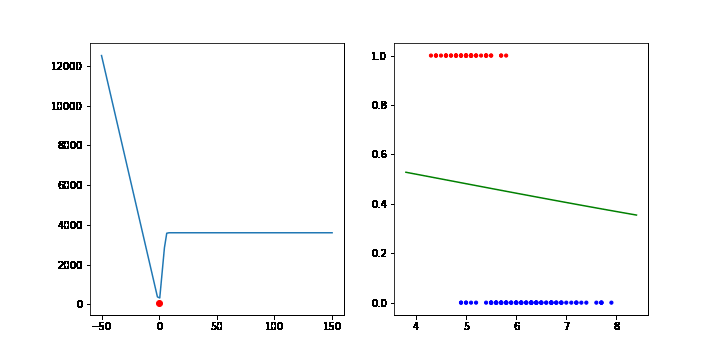
데이터수가 적어서 그런지 생각과 조금 다르게 움직이지만 분류가 되는 것을 확인할 수 있습니다.
5) 확률적 경사하강법(Stochastic Gradient Descent)
여태껏 작성한 경사하강법은 전체 데이터에 대하여 가중치를 적용하기때문에 데이터가 많을수록 시간이 오래 걸리는 단점이 있습니다. 이런 점을 보강하는 알고리즘이 여러 가지 있는데 그 중 하나가 확률적 경사하강법(SGD) 입니다. SGD는 랜덤적으로 추출한 하나의 데이터에만 가중치를 적용합니다. 즉, 속도가 훨씬 빨라집니다. 그러나 정확도는 BGD에 비하여 떨어집니다.


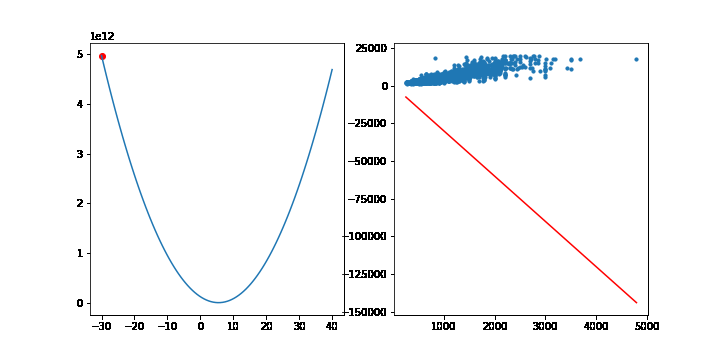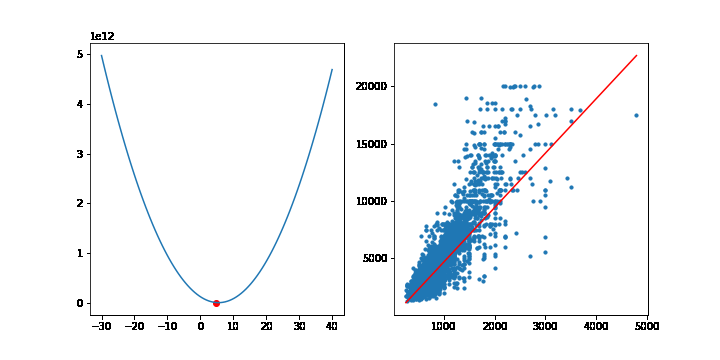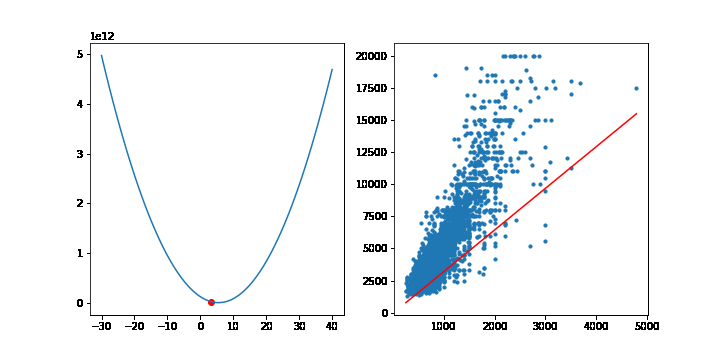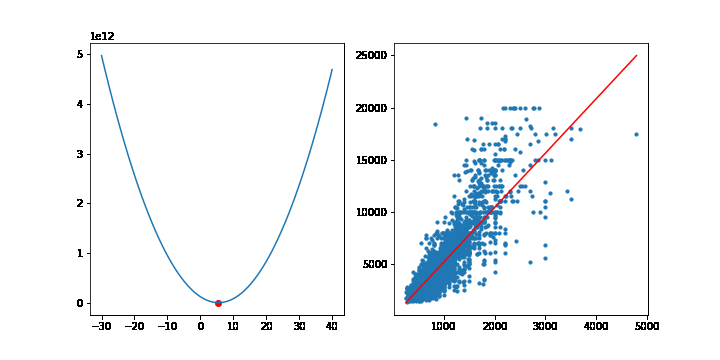
|  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟