
2) CART 알고리즘
CART는 Classification and Regression Tree의 약자로, 이름 그대로 분류와 회귀가 모두 가능한 결정트리 알고리즘입니다. ID3이 엔트로피를 사용하여 분류를 했다면 CART는 지니계수를 사용합니다. 또한 ID3은 모든 클래스로 분기하는 반면 CART는 yes 또는 no 두 가지로 분기합니다.
CART 알고리즘의 비용함수는 다음과 같습니다.
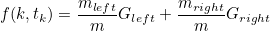
k는 특성이고 tk 는 특성에 대한 임계값을 말합니다. 또한 m은 샘플수를, G는 지니계수(불순도) 입니다. 지난번 사용한 타이타닉 데이터를 통해 분기해보겠습니다.
class 특성을 예로 들면 First, Second, Third 3가지 속성이 있습니다. 먼저 First class에 대한 생존여부의 지니계수를 구하겠습니다. First class에 속한 사람들과 나머지 class에 속한 사람들로 나눠줍니다. 
각각 지니계수를 구하여 비율만큼 곱하여 더합니다.

해당값이 First class에 대한 지니계수입니다. Second class와 Third class도 동일하게 구합니다. 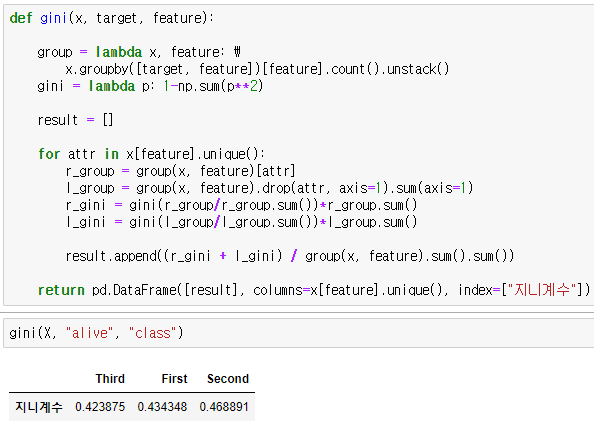
불순도가 낮을수록 복잡도가 작다는 뜻이므로 더 분류가 잘된 경우입니다. class 특성에서는 Third속성의 지니계수가 제일 작으므로 Third와 Third가 아닌 그룹으로 분기합니다.
아직 class로 분기한다는 뜻은 아닙니다. 다른 특성들도 동일하게 지니계수를 구해야합니다. 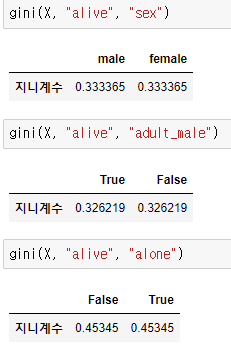
adult_male 특성의 지니계수가 가장 낮습니다. 속성이 2가지로 분기하는데 속성도 2개이므로 두 속성의 지니계수는 동일합니다.
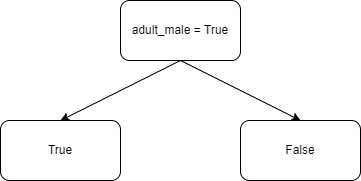
이제 adult_male이 True인 데이터로 동일하게 분기하고 adult_male이 False인 데이터에서도 동일하게 분기합니다.
속성이 연속형 자료라면 어떻게 기준점을 정해야할까요? iris 데이터를 통해 확인해보겠습니다.
데이터를 불러옵니다. 
4가지 특성이 모두 연속형 자료입니다. 우선 sepal_length를 기준으로 설명하겠습니다. sepal_length를 오름차순 또는 내림차순으로 정렬합니다.
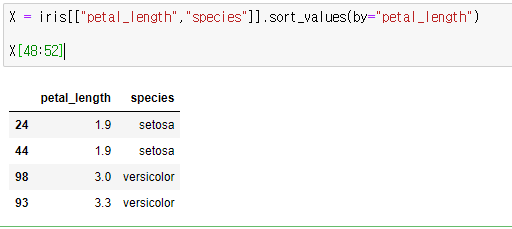
그런다음 species가 변경되는 지점의 평균 길이를 구합니다. (1.9 + 3.0) / 2 = 2.45 가 기준점이 됩니다. 2.45를 기준으로 2.45보다 작거나 같은 그룹과 2.45보다 큰 그룹으로 나누어 지니계수를 구합니다.
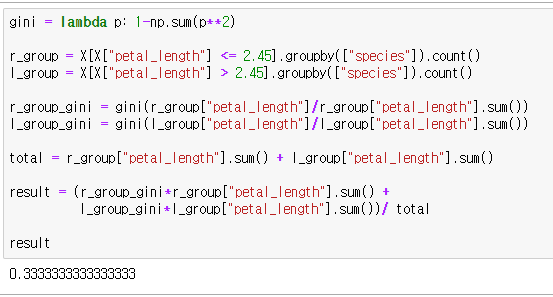
모든 변경지점에서 지니계수를 구합니다. 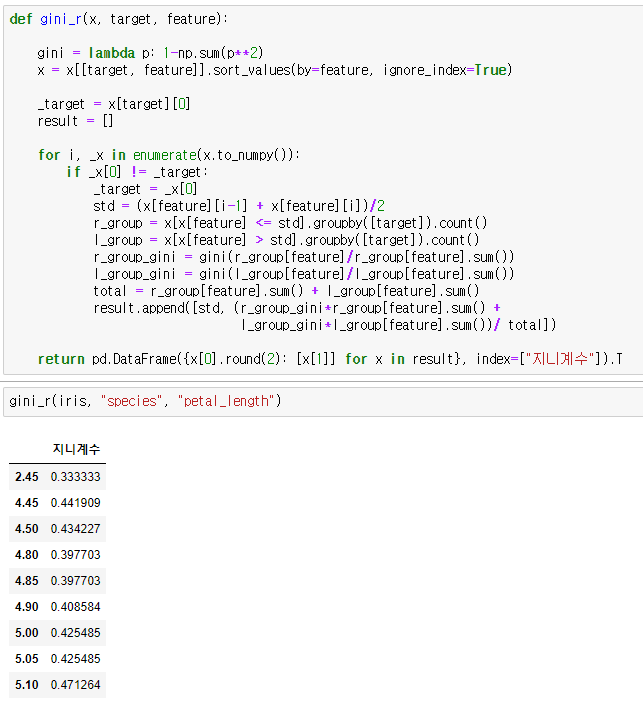
2.45에서 지니계수가 가장 낮습니다. 그러므로 petal_length로 분기한다면 2.45를 기준으로 이분됩니다. 모든 특징에서 반복된 과정을 거쳐 가장 낮은 지니계수를 지닌 특성의 기준점으로 분기합니다.
사이킷런 모듈의 결정트리 모델이 CART 알고리즘을 사용합니다. 
DecisionTreeClassifier 분류기를 훈련시키고 export_graphviz 함수를 통해 dot 파일을 만들어서 이미지를 형성할 수 있습니다.pydot는 conda 환경에서 conda install pydot 명령어를 통해 설치하면 되는데 저는 오류가 나서 파이프를 통해 pydot_ng 모듈을 설치했습니다. 분류기의 하이퍼 파라미터로 max_depth를 설정하는데 가지의 깊이가 어디까지 분기될것인가를 설정합니다.
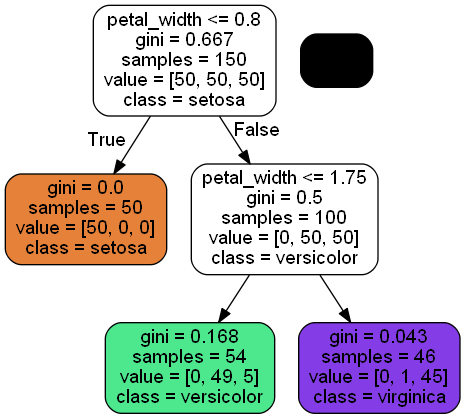
petal_length와 petal_width 특성만으로 훈련하여 플롯을 그려보겠습니다.

depth를 다르게 하여 확인해봅시다. 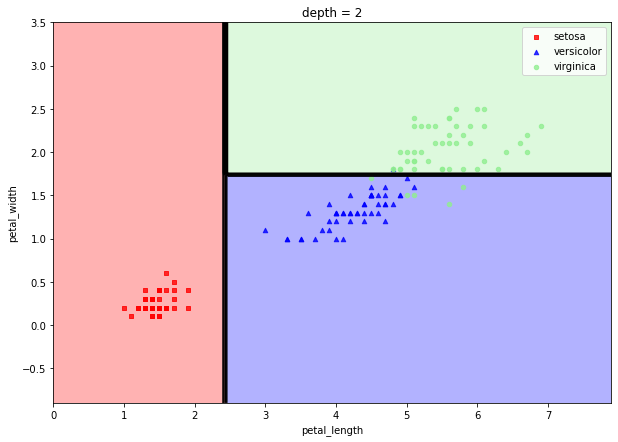
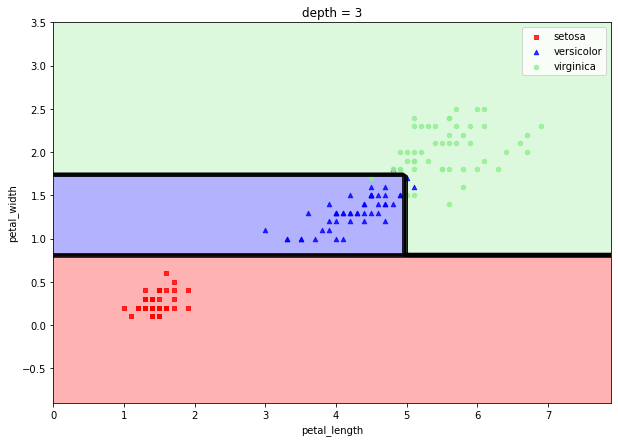
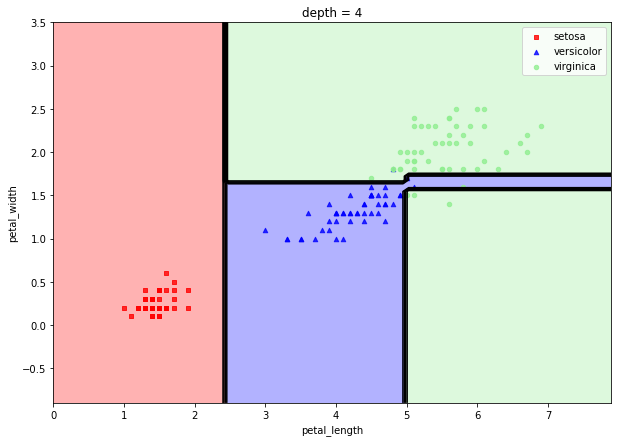
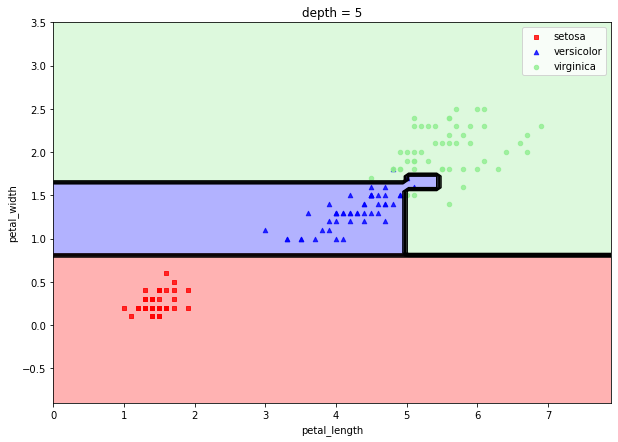
depth가 깊어질수록 오버핏이 됩니다. 이전에 말했듯이 오버핏이 된 모델은 분산이 커서 예측력이 떨어지기때문에 depth를 적절히 조절하여 일반화된 모델을 만드는 것이 좋습니다. |  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟