
통계학을 설명할때 마지막에 카이제곱 분포에 간단히 설명했는데 이번 글에서 좀더 자세히 알아보겠습니다.
χ²-값은 표본 분산을 표준화한 값이라고 보면 됩니다. 즉, X-값은 편차를 표준화한 Z-값이라 볼 수 있습니다.
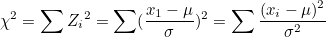
이 식에서 모평균 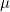 대신에 표본평균 대신에 표본평균 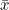 로 바꿔주면 χ²-값들은 자유도가 n-1인 χ²-분포를 따르게 됩니다. 로 바꿔주면 χ²-값들은 자유도가 n-1인 χ²-분포를 따르게 됩니다.
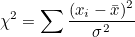
표본분산 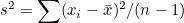 이므로 이므로 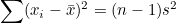 가 됩니다. 이 식을 위의 식에 대입하여 다음과 같이 정리할 수 있습니다. 가 됩니다. 이 식을 위의 식에 대입하여 다음과 같이 정리할 수 있습니다.
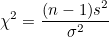
이 값들의 확률분포는 자유도가 n인 χ²-분포(χ²-distribution)를 따릅니다.
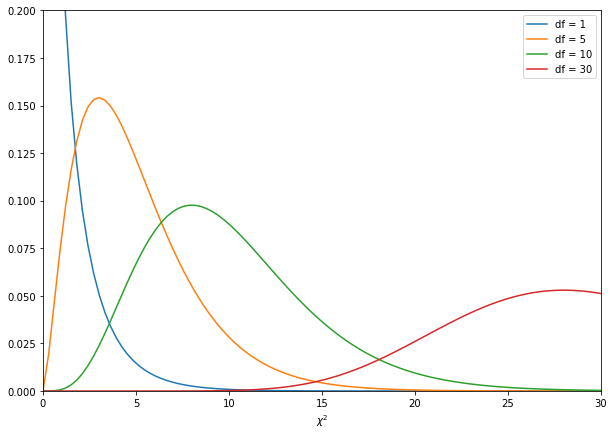
χ²-값은 편차의 제곱값이므로 양수만 존재합니다. 자유도가 작으면 분포의 정점이 왼쪽으로 치우쳐있지만, 자유도가 커질수록 완만한 모양의 정규분포에 가까워집니다.
χ²-값은 모분산 검정이나 적합도 검정, 교차분석에 이용됩니다. 적합도 검정(test for goodness of fit)은 하나의 범주형 특징을 통해 관측값과 기대값의 분산을 비교하는 것이고, 교차분석(cross-tabulation analysis)은 두 범주형 특징의 관계를 분석하는 것입니다. 여기서 교차분석을 χ²-검정(chi-square test)이라고 부릅니다. χ²-검정에는 독립성 검정(test of independence)과 동질성 검정(test of homogenity)이 있습니다.
적합도 검정과 교차분석에서 사용하는 χ²-값은 다음과 같습니다.
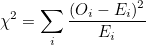
이 식을 피어슨 카이제곱 통계량(Pearson’s chi-squared statistics)이라고도 합니다. 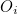 는 관측값이고 는 관측값이고 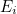
는 기대값입니다.
해당 식은 다음과 같이 변형할 수 있습니다.
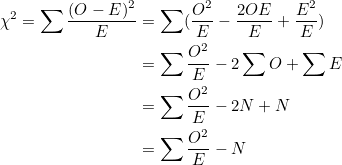
N은 전체 관측값을 말합니다.
1) 적합도 검정(test for goodness of fit)
적합도 검정은 범주형 변수가 한 가지인 일원분할표에서 χ²-검정에 의해 각 범주의 관측치와 기대치가 일치하는지를 검정합니다.
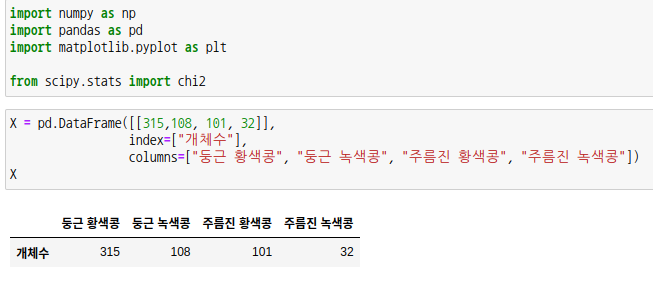
생물학 시간에 많이 본 멘델의 유전법칙에 따른 비율을 검정해보도록 하겠습니다.
알고 있겠지만 우열의 법칙과 분리의 법칙, 독립의 법칙에 의해 개체수는 9:3:3:1로 분리됩니다.
다음과 같이 가설을 설정합니다.
H0 : 콩의 분리비는 9:3:3:1이다. H1 : 콩의 분리비는 9:3:3:1이 아니다. |
개체수에 대한 기대값을 구해줍니다. 전체 개체수를 해당 비율로 나누면 됩니다.

자유도는 개체수에 대한 자유도가 아니라 범주의 수에 대한 자유도 입니다. 해당 일원 분할표에서는 4개의 범주가 있는데 3개의 범주에 대한 기대값이 정해지면 나머지 하나의 기대값은 자연스럽게 결정됩니다. 4개의 범주에 대한 기대값의 합은 전체 개체수와 같기때문입니다. 즉, 다시말하면 자유롭게 정할 수 있는 숫자의 개수는 3개이므로 자유도는 3이 됩니다.
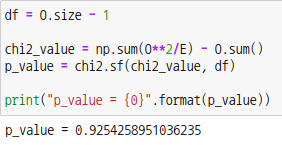
p-값이 유의수준 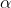 =0.05 보다 크므로 귀무가설을 채택하여 콩의 분리비는 9:3:3:1이 됩니다. 이때 적합도는 92.5%입니다. =0.05 보다 크므로 귀무가설을 채택하여 콩의 분리비는 9:3:3:1이 됩니다. 이때 적합도는 92.5%입니다.
scipy모듈의 서브패키지 chisquare를 사용하여 적합도 검사를 할 수도 있습니다. 파라미터로 관측값 배열과 기대값 배열을 넣어줍니다.
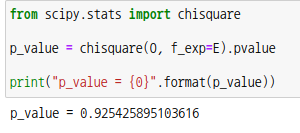
2) 독립성 검정(test of independence)
독립성 검정은 교차분할표에서 χ²-검정에 의해 두 범주형 특징 사이의 관계를 검정하는 것입니다.
바로 예제를 통해 확인해보겠습니다. seaborn 모듈에서 titanic 데이터를 불러옵니다.
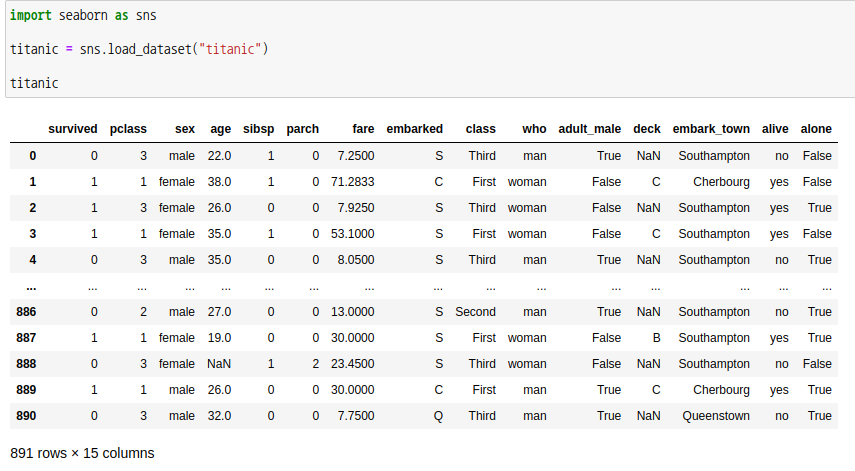
승선지(embarked)와 등급(class)의 관계를 확인해보도록 하겠습니다.
H0: 승선지와 등급은 서로 독립적이다. (상관관계가 없다.) H1: 승선지와 등급은 서로 독립적이지 않다. (상관관계가 있다.) |
데이터를 가공하여 교차분할표 O를 만들겠습니다.
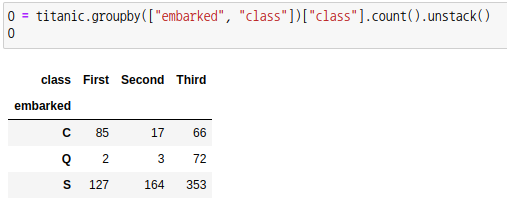
각 관측값에 대한 기대값 배열을 만드세요.

기대값은 같은 행렬의 합을 곱하여 전체값으로 나눠주면 됩니다. 예를 들어 1행 1열의 기대값은 1행의 전체값 (85 + 17 + 66)과 1열의 전체값(85 + 2 + 127)을 곱하여 전체값 N으로 나눠줍니다.
자유도 df는 (행 크기 -1) * (열 크기 -1) 입니다.
p-값을 보면 유의수준 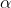 =0.05 보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다. =0.05 보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다.
즉, 승선지와 등급은 독립적이지 않고 상관관계가 있습니다.
마찬가지로 scipy모듈의 서브패키지 chi2_contingency 를 사용하여 적합도 검사를 할 수도 있습니다. 파라미터로 데이터프레임타입인 교차분할표를 넣어주면 χ²-값, p-값, 자유도, 기대값이 순서대로 출력됩니다.
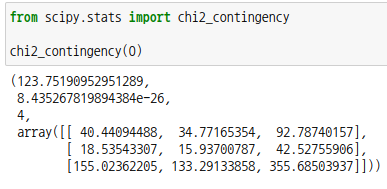
옵션으로 파라미터 correction을 설정할 수도 있습니다. 이것은 χ²-값을 보정해 줄것인지 여부를 설정합니다. 자유도가 1인 경우 χ²-값은 약간 높게 계산됩니다. 그러므로 다음과 같이 절대값 | O - E | 에서 0.5를 뺀다음 제곱하여 보정해주는데, 이것을 야트보정(Yate's correction)이라고 합니다.
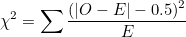
3) 동질성 검정(test of homogenity)
동질성 검정은 범주간 비율이 동일한지를 검정합니다. 검정 방법이 독립성 검정과 동일하여 혼동하여 사용하기도 합니다. 그러나 동질성 검정은 "비율이 서로 같은지"를 검정하고, 독립성 검정은 "관계가 있는지"를 검정합니다.
titanic 데이터에서 등급(class)에 따라 생존율이 차이가 있는지를 확인해보겠습니다.
H0: 등급에 따른 생존률에 차이가 없다. H1: 등급에 따른 생존률에 차이가 있다. |
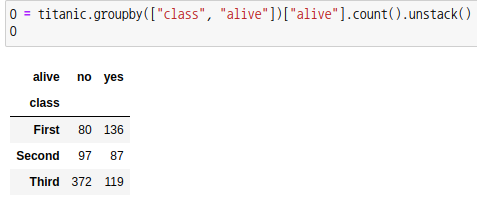
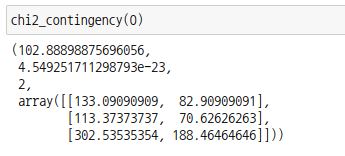
p-값을 보면 유의수준 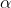 =0.05 보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다. =0.05 보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다.
즉, 등급에 따른 생존률에 차이가 있습니다. |  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟